Розв’язування задачі лінійного програмування симплексним методом. Геометрична інтерпретація симплексного методу
Симплекс-метод — метод розв'язання задачі лінійного програмування, в якому здійснюється скерований рух по опорних планах до знаходження оптимального розв'язку; симплекс-метод також називають методом поступового покращення плану. Метод був розроблений американським математиком Джорджем Данцігом у 1947 році.
Описання методу
Нехай невироджену задачу лінійного програмування представлено в канонічному вигляді:
- Неможливо розібрати вираз (невідома помилка): \sum_{j=1}^n c_jx_j \to \max
,
- Неможливо розібрати вираз (невідома помилка): \sum_{j=1}^n A_jx_j = B,\quad x_j \ge 0,\quad j = 1, 2, \ldots, n,
де X = (x1, …, xn) — вектор змінних, C = (c1, …., cn), B = (b1, …, bm)T, Aj = (a1j, …, amj)T, j = 1, …, n — задані вектори, T — знак транспонування, та
- Неможливо розібрати вираз (невідома помилка): \bar{X} = (\bar{x}_1, \ldots, \bar{x}_m)
відмінні від нуля компоненти опорного плану, для полегшення пояснення розташовані на перших m місцях вектору X. Базис цього плану — Неможливо розібрати вираз (невідома помилка): \bar{A} = (A_1, \ldots, A_m)
. Тоді
- Неможливо розібрати вираз (невідома помилка): \sum_{i=1}^m A_i \bar{x}_i = B
, (1)
- Неможливо розібрати вираз (невідома помилка): \sum_{i=1}^m c_i x_i = \bar{z}_0
, (2) де Неможливо розібрати вираз (невідома помилка): \bar{z}_0
значення лінійної форми на даному плані. Так як вектор-стовпці матриці A лінійно незалежні, будь який із векторів умов Aj розкладається по них єдиним чином:
- Неможливо розібрати вираз (невідома помилка): \sum_{i=1}^m A_i x_{ji} = A_j, \qquad j = 1, \ldots, n
, (3)
- Неможливо розібрати вираз (невідома помилка): \sum_{i=1}^m c_i x_{ij}, \qquad j = 1, \ldots, n
, (4) де xij коефіцієнт розкладання. Система умов
- Неможливо розібрати вираз (невідома помилка): \sum_{i=1}^m A_i x_i + A_k x_k = B, \qquad k \ge m + 1
, (5)
zk ≥ 0, xj = 0, j = m + 1, …, n, j ≠ k (6)
при заданому k визначає в просторі змінних задачі промінь, який виходить із точки, яка відповідає опорному плану, що розглядається. Нехай значення змінної xk при русі по цьому променю дорівнює θ, тоді значення базисних змінних дорівнюють xi(θ). В цих позначеннях рівняння (5) можна представити у вигляді
- Неможливо розібрати вираз (невідома помилка): \sum_{i=1}^m x_i (\theta) A_i + \theta A_k = B
. (7) помноживши рівняння (3) на θ при j = k та віднявши від рівняння (1), отримаємо
- Неможливо розібрати вираз (невідома помилка): \sum_{i=1}^m (\bar{x}_i - \theta x_{ik}) A_i + \theta A_k = B
.(8) Із рівнянь (7-8) отримаємо
- Неможливо розібрати вираз (невідома помилка): x_i (\theta) = \bar{x}_i - \theta x_{ik}, \qquad i = 1, \ldots, m
. (9) Оскільки xi(θ) при θ = 0 визначають план задачі, то найбільше θ, яке не порушує обмеження xi (θ) ≥ 0, визначається із умови
- Неможливо розібрати вираз (невідома помилка): \theta_0 = \min_{i \in I} \frac{\bar{x}_i}{x_{ik}}
. (10) де I = {i | xik > 0}.
В силу невиродженості задачі мінімум досягається не більш ніж для одного i = J та θ > 0. Значення лінійної форми при θ = θ0 визначається із рівнянь (9), (4), (2)
- Неможливо розібрати вираз (невідома помилка): z_0 (\theta_0) = \sum_{i=1}^m c_i x_i (\theta_0) + c_k \theta_0 = \bar{z}_0 - \theta_0 \Delta_k
, де Δk = zk — ck. Очевидно, Δj = 0 для j = 1, …, m.
Нехай Неможливо розібрати вираз (невідома помилка): \bar{A} = E — початковий базис із m одиничних векторів. Всі дані задачі записуються у вигляді симплекс-таблиці (першої ітерації обчислювального процесу). Симплекс-алгоритм розв'язання задачі лінійного програмування складається із наступних операцій:
- знайти Неможливо розібрати вираз (невідома помилка): \Delta_k = \min_j\Delta_j
. Якщо Δk = 0, тоді план, який розглядається оптимізовано; якщо Δk < 0, вектор Ak вводиться в базис;
- знайти θ0 та l, для якого Неможливо розібрати вираз (невідома помилка): \theta_0 = \bar{x}_l / x_lk
, із формули (10). Якщо I = Λ — порожня множина, лінійна форма необмежена зверху; якщо I ≠ Λ вектор Al виводиться із базису;
- за знайденими l, k обчислити нові значення елементів таблиці за формулами
- Неможливо розібрати вираз (невідома помилка): x_{ij}' = \begin{cases} x_{ij} - \frac{x_{lj}}{x_{lk}} x_ik, & \mbox{if } i \neq l; \\ \frac{x_{lj}}{x_{lk}}, & \mbox{if } i = l; \end{cases}
(12)
- Неможливо розібрати вираз (невідома помилка): i = 1, \dots, m + 1,\quad j = 0, 1, \dots, n
, де Неможливо розібрати вираз (невідома помилка): x_{i0} = \bar{x}_i,\; x_{m+1\, 0} = \bar{z}_0,\; x_{m+1\, j} = \Delta_j
та перейти до виконання операції (1) з новими значеннями всіх xij = x'ij.
Перетворення (12) замінює вектор коефіцієнтів Xk = (x1k, …, xmk) на одиничний вектор Xk з xlk = 1. В силу монотонного збільшення x0 повернення до вже пройденого плану неможливе, а із скінченності кількості опорних планів випливає скінченність алгоритму.
Початковий опорний план з одиничним базисом можна отримати, розв'язавши описаним алгоритмом допоміжну задачу
- Неможливо розібрати вираз (невідома помилка): \sum_{i=1}^m (- y_{n+i}) \to \max
, при обмеженнях
- Неможливо розібрати вираз (невідома помилка): \sum_{j=1}^n a_{ij}x_{j} + y_{n+i} = b_i,\quad i = 1, \dots,
- Неможливо розібрати вираз (невідома помилка): y_{n+1} \geq 0, i = 1, \dots, m
- Неможливо розібрати вираз (невідома помилка): x_j \geq 0, j = 1, \dots, n
, яка містить одиничний базис, який складається із векторів An+1, …, An+m. Цим векторам відповідають штучні змінні із значеннями Неможливо розібрати вираз (невідома помилка): \bar{y}_{n+i} = b_i , i = 1, …, m. Якщо в оптимальному розв'язку цієї задачі Неможливо розібрати вираз (невідома помилка): \sum_{i=1}^m y_{n+i} > 0 , вихідна задача не має розв'язку. Якщо ж Неможливо розібрати вираз (невідома помилка): \sum_{i=1}^m y_{n+i} = 0
та задача невироджена, оптимальний базис складається лише тільки із векторів вихідної задачі, які за формулами (12) перетворені в одиничну матрицю. Якщо задача має невироджені плани, значення z0 може не збільшуватись на ряді ітерацій. Це відбувається через те, що значення відповідних Неможливо розібрати вираз (невідома помилка): \bar{x}_l
дорівнює нулю та визначається неоднозначно. В таких випадках монотонність методу порушується і може трапитись зациклювання, тобто, повернення до вже пройденого базису. Невелика зміна вектора обмежень задачі, яка полягає в заміні величин bi на bi + εi, де εi достатньо малі, при вдалому виборі εi не змінюють множину векторів оптимального опорного плану вихідної задачі і робить її невиродженою.
Описаний вище алгоритм називається першим (або прямим) алгоритмом симплекс-методу. Також відомий другий алгоритм (алгоритм із оберненою матрицею). В ньому перетворюється лише матриця A-1, обернена до базисної матриці.
Приклад
Файл:Приклад розв(симплекс метод).doc
Геометрична інтерпретація
Геометричну інтерпретацію симплекс-методу подамо способами.
1) ілюструється зміна базису, яка здійснюється вибором векторів, які включаються до базису та виключаються з нього.
2) процес симплексного методу інтерпретується як послідовний рух через сусідні кутові точки багатогранника розв’язків, що пов’язано зі збільшенням (зменшенням) цільової функції.
Дві кутові точки назвемо сусідніми, якщо вони розташовані на одному ребрі багатогранника.
Розглянемо задачу максимізації лінійної функції
Неможливо розібрати вираз (невідома помилка): Z = c_1x_1 + c_2x_2
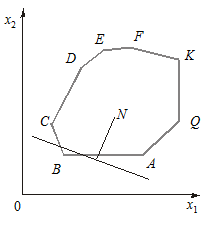 1)
Початковий опорний план відповідає кутовій точці А.
Другий крок симплексного методу приведе до точки Q, (Неможливо розібрати вираз (невідома помилка): Z(Q)>Z(A)
1)
Початковий опорний план відповідає кутовій точці А.
Другий крок симплексного методу приведе до точки Q, (Неможливо розібрати вираз (невідома помилка): Z(Q)>Z(A)
),
Третій — до точки K, де лінійна функція набуває максимального значення.
2) Якщо початковим опорним планом є В, то включення вектора до базису за критерієм Неможливо розібрати вираз (невідома помилка): min \theta_j(Z_j - c_j)
приводить до того, що пряма Неможливо розібрати вираз (невідома помилка): c_1x_1 + c_2x_2 = const проходитиме через точку С і алгоритм симплексного методу приведе до точок С, D, E, F, K, тобто для отримання оптимального плану необхідно буде виконати ще чотири ітерації.
Отже, очевидно, що застосування симплексного методу не дає змоги одразу перейти від опорного плану (точки В) до оптимального (точки К).
Фактично розв’язок отримують, рухаючись вздовж межі (ребер) простору розв’язків, причому не завжди такий шлях буде най-коротшим.
Кількість ітерацій за реалізації симплексного алгоритму визнача-ється вибором початкового опор¬ного плану та кількістю кутових точок на шляху прямої Неможливо розібрати вираз (невідома помилка): c_1x_1 + c_2x_2 = const
.
Література
Енциклопедія кібернетики в 2 т. / За ред. В. М. Глушкова. — Київ: Головна редакція Української радянської енциклопедії, 1973.
Кратко М. Як створювалася україномовна «Енциклопедія кібернетики»// Аудиторія: освітній студентський тижневик. – 19–25 листопада 2009р. – ч. 31 (2671)– С. 6–7.
